出自:西南石油大学土木工程施工与组织(专升本)

新课标中提到的“四基”是指:基础知识、基本技能、基本思想和基本方法。
·正确
·错误
逻辑推理是主要包括归纳、类比和演绎三种推理形式。
·正确
·错误
高中数学课程由必修课程、选择性必修课程和选修课程组成。
·正确
·错误
资本的价值构成决定其技术构成。( )
·正确
·错误
经济基础是社会发展的最终决定力量。( )
·正确
·错误
唯心主义否认思维和存在的同一性。( )
·正确
·错误
社会主义代替资本主义是历史的必然,因此就不可能有反复。( )
·正确
·错误
马克思主义是为全人类服务的。( )
·正确
·错误
劳动力的使用价值是其价值的源泉,并且是大于它自身价值的源泉。( )
·正确
·错误
剩余价值的产生,既不在流通领域,又离不开流通领域。( )
·正确
·错误
马克思主义认为,实践的主体和客体之间的主要包括( )
·认识关系
·依存关系
·互动关系
·实践关系
下列说法中,关于“社会存在”的正确理解是( )
· 社会存在也就是指社会物质生活条件,或者说是社会生活的物质方面
· 社会存在包括物质生活资料的生产及其生产方式
· 社会存在是由社会意识所引导和决定的
· 地理环境和人口因素也属于社会存在的范畴
下面关于社会意识的理解中,正确的是( )
· 社会意识是社会存在的反映
· 社会意识包括政治法律思想、道德、宗教、哲学和艺术等方面
· 社会意识是具体的、历史的
· 在阶级社会中,社会意识形式是具有阶级性的
设( 4,6,4,3,5,4,5,8,4,7 )是来自总体 的一个样本值,则样本均值=()。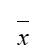
·2
·3
·4
·4

····<img src="https://u.qsxt.info/degree/school_4595/39538220_20240114111851736_229.jpg"

····<img src="https://u.qsxt.info/degree/school_4595/39538220_20240113170246510_882.jpg"
以<img data-latex="A" data-qs-formula="true" src="data:image/png;base64,iVBORw0KGgoAAAANSUhEUgAAABcAAAAZCAYAAADaILXQAAAAAXNSR0IArs4c6QAAAZNJREFUSEvt1T9IVlEYx/GPJYRbCdkQ4RQWREOrYCDoWDSYURFtRkuEgrgkKdQiloNC4CBF0h8coqWpIRqac6nRJUGRQNCKHLoPHOSq11d9ry84dOAO955zvuc5v+f5PbdODUddDdkOLLwevTiEx0UKlIm8FS/xAffxa/MB1cKP4Rm6MIl7WN0PeAR0AxdwDV/T+9J+wE/jFmYwhRVcx1xZeCSxH+8xj2kcRze+l4W34ywmcBQv0IZOfCkDjyT2ZdCnWEQDnmQ36MFFfKoWHkm8nXT9mCDxbTA9N1NZbuDvthRbcAUjWMsRBvAId1Jp7hl+JHPhEA4nOfKAc4ioH2Tzw9XI0oHGLJGvCyx+Ce9SgqMV/M6v2UmWJtzFKJYL4NECPidJtrSASvCYC/BsUSWkg87gDX4UubQS/Hyy90P82abvR6JDrp8JHoesj+3gJzPnjeNtUYnl9oc7w6UncDUL5lsl+KlklMtoTpKM4Tn+5jZGLqK/hHnCXHHLaL2h/6tMzoVYu1NCS/0F/8ML5aupLP8A7EJDGtmvp98AAAAASUVORK5CYII=" style="vertical-align: middle;">表示事件“甲种产品畅销,乙种产品滞销"，则其对立事件为（ C ）。
·“甲种产品滞销，乙种产品畅销”
·“甲、乙两种产品均畅销”
·“甲种产品滞销或乙种产品畅销"
·“甲种产品滞销”

·正确
·错误

·正确
·错误

·正确
·错误
在对单正态总体<img data-latex="N(\mu ,{\sigma }^{2})" data-qs-formula="true" src="data:image/png;base64,iVBORw0KGgoAAAANSUhEUgAAAFYAAAAdCAYAAAAwyZtYAAAAAXNSR0IArs4c6QAABmxJREFUaEPtmneIPEUQhb8fijkroigoKiYUQQyYwYgJMeesmHPOOeesmCMGRFFQEcwJUUQFxYwBxT/MEcXU31G9zM3NzM7e3t55cA3HHbs93V2vq169qrlpTI2BIDBtIKtOLcoUsANygokEdi7gZ+DvAdnWz7KLAkcAnwPrAW8BZwO/xqKzA38Cf9RtMhHAuueB6aDTA1cC//aDwACenTNAvBp4H1gIuAd4DTguHGGJBPIxwHnAp1VnmAhgtwdWBk5quvEBANZ2yXWBbYFDgL/ioTOAjYGtgS/iszWTR+8FHA18V168G7ArAbsAywKrpUV+SQvvDTxWWmju2GBDYDbAMH8ZuLk0dxngXOBY4MO2lo7zPG24KXnmKcDtsbfeuU9goec6xE47Zk5/C/ywyOsGbLZpN+ASYL7Y9KDgmLLNawCXJu48Cnix9OUMsYbhZZhNliFGnldK0EOL3ulnNwDnAK8UDWoL7AXA98Du8fDOwBsVyBhG26XND60AfkXgfOBg4IPJgiqwKnANcGGK3Psrzq1ny8t6dcdr2wBrWOuF3prkLXDyT5XXmUl/B66vOIAbm20F9v+WsOrueR7gusSvrybwLqs59zrAqeHNn+WF2gC7QvLWw0J+bB4bPQ/sWgoLQ90s760+XTqpN3ob8BBwxyTx1hkjwkxWdaBqivR4Z+DySC/AmglXCW9dMqTHIoC8+3gBpAWAi4DjgS9L4C2VOOrGpAJOAF6aBMDqcEbfP8AV4ak7Bo+W5ZVzjdCv07zTegHWjPdOeKKLCJ7JyWRW5BUT105xIMVzcci9p8dlVOq+wmQjRO9+Ii6iuM5+gKEnJWXZ08s9GTlz1DzwW6K4b+O7bSJZSXcWMD6nmvGn7DQ+ojPpPJ5vyPZuVGCFYRhcFdWHzwiS4ewNCWRORPsnsJ0v8OWxVfCyt+5zTcNIUOYcUOJqQ+6uAEadWWVg1braqIQ6MVHU2g0bKyH3SLYtFhe7dGnug8CeUS2Wl9H2jeL5H9sA6y2cHF74Tawmocspm4RKEGQPf3l4WZEe8gH07NWLG9cYmKXNFuHdRa7Wk++OCqjjGV0uabrQ1xpuElKfWoYacYdHhWVi7nfoOBYKnQvv5rFWG962fFMcZna92ESltlMkSw1yTFWotwW2yStVI/eFKK+KiipwlIdqTIH02TzyPioYvXTIy/oYAisddCqzbsA6+auKTJ69x9A3dOUnKxMvwL/Loy2wVndGwwtFvorFBFMQykmzDo+caN8OWik2TLJKUeAXy9TRYtsTsLMEvxo+uYzLGyutFM2CqYZTvy1ezIqlE47goBoLMr8eGXvnaWppeVfloed29GIDEkaVEWREPVqaJ6APAD9FmZpprh9g1fadHNLksUoqD2Y9XLWxmvaWZOi7SdN+DDwMdHRc6YQjOKjGAullywZ+1fu8zKqoKC7pxVtqLg+Y4cv0lBPwveWKaZTIjojIJmDdfLPgp6pKKbfTzLRvAjtEm63qbIa4LTaTjr2CqpF5z99lMDK/qoMti5WA6uEna9bKoe7XZQ7NktFEY4Q8N0owi495nvmDcoY+bwLWW7ARXVWe5kWtk89MntEkRZybL0FQqlSDc2wlKqdMJEXeswIycwuCPQq7ZtbtGlNHCVldLBzK5YcCCtb+RtqtkXD7La+lzEyXStNGYBeMjT1AVeMhP5+TjTKoU3VUeEDmZDVvXUbP/PpeAGiTR4D0ODl63iijNUS1kosTy20loRysVs3FiZ1/9/J7k6HDtqVl9zMBau0bgB68WMq0oDmrWMqXPXa5ROgmjvVD7/kqwvafHvNJxWazhkfLr3pt07Cvu2lwZH7FUZwvv0ongmCD+dkQ668DT4XmdL4ednFKOh8F8FZHvpGooqMNUiGxb3TirLj80bucO1bDXGOPelhLsZvcGqvNMx1olHRQ5rXMrzbM22b9fDbBMrzlZT1nWF90LA1oiETfiQ3r9o0nsJ7LMtVS0TAu9hMyv8qfbauqop3SgxemBKxLjoPAWCpU62uXer8zxhtYy2G7RXqW4Z1H5lelXduqqmiHpbfNdZ+voplBgGpS1Rb5uljVDe013sC6p284TXRmdXnSUadf2wCiDb6YNDE2Jdo2a7Wd456WyQ5L+RHKYiKA9TCWxOpIw9eep8lopiiJe63bbdisNc5vfe1kWTJfW/d/ERMFbFvPmLTz/gPs1GstmDwetwAAAABJRU5ErkJggg==" style="vertical-align: middle;">的假设检验问题中，<img data-latex="T" data-qs-formula="true" src="data:image/png;base64,iVBORw0KGgoAAAANSUhEUgAAABcAAAAZCAYAAADaILXQAAAAAXNSR0IArs4c6QAAAaZJREFUSEvt1DtoVUEUheEvCClUBINFQBBBSCUYYiXpBBErwUISg2Ik+AArwcI0ojaihaiFChLiCyEP21RRm5QRBAsflUUgiKCQYGERnS0jXA735ExzrTzlzJl/1l6z1+7Swa+rg2z/HN6DCRzGWyxiFRswiH58wCv8xGbsxR7M4xi+hCPtlO/DHVzHC/zK1m3EwwQexjncb7E0Lr6GPoxipQ5+EZvSxVdawPHvTsxgK05gofJeR9LagXzxn62q8oCG4rupvI+Vw4fwGO+y+uU28F1J2M2/61V4+HY8eTme/Ww9HxXdSBVM4kzN/mdMrQePsl9XVHXjAU7iAm61aeGDye+Av6+D17X9dkynLtqR/X5Zko/SPt+f/V7C0aywkV8KP4t7eI4x/Ggk1/R59VwIiJ4+jUu5m0rYRfHvzYp3Z7/nisiFyiOxT3LqhnL0i/glnkcaH2G2Ndol9BJ4pPU8rqZxcLkEWtrn2/A0T8MIUKgv/pqUD+BZpo3gTTG55kFP5dkcczom4Ras4Ts+JYu+psl4G9+aLmpS3nR+3f3/8Lb2dNSW37l5RRq6UiFBAAAAAElFTkSuQmCC" style="vertical-align: middle;">检验法解决的问题是（ ）。
·已知方差，检验均值
·未知方差，检验均值
·已知均值，检验方差
·未知均值，检验方差

····<img src="https://u.qsxt.info/degree/school_4595/39538220_20240114111146812_801.jpg"
假设检验时，若增大样本容量，则犯两类错误的概率（ ）。
·有可能都增大
·有可能都减小
·有可能都不变
·一定一个增大，一个减小
在下列数组中，（ ）中的数组可以作为离散型随机变量的概率分布。
·<img data-latex="\frac {1} {2},\frac {1} {3},\frac {1} {4},\frac {1} {5}" data-qs-formula="true" src="data:image/png;base64,iVBORw0KGgoAAAANSUhEUgAAAEMAAAAkCAYAAADSO4eRAAAAAXNSR0IArs4c6QAABGFJREFUaEPtmWuoVkUUhh81LxkWYmWZaAUaVlqRlCEqgknZjzAStFIjtTJKKbKyzAsK3i+hEEZFaNLF/ghKCmUWFJEh2QWzCxGZYRKGFyzztl5YY+Nm72/P93n+nMOeP4fz7TVrr/XOu95ZM7sV1TiDQKsKi/8RqMCI2FAGxpXANGAGcKABFsn/COBaYHED88OUc41Dfkp9FIHRA7gHuA64HBjbABiDgSHAQOBjYH4DYDRFHMk+ypihRKY3CEbI/UVj1vEGwQg+miKOUh8VGHVoRimaCdSvmBGBVIFRgZFfMxUzKma0UGZ0Am6wZmkoMAaYC3wHfAucTNhBZNIT6A087PavALuAPYnzZdYUcST7KOsz6oi7+ZtWYNTRdDX/5a4jg5gZreuYJ9M87WjWPmIwLgImJwKy1Y7mX+TY6rjeL9HHh8D2HNu7gL6JPo4CL+XYdgYeSfTxAfClbCvNqDQjnzNFzAg3VFcBbYGbgEXeZySyjwu8x/gT6G43Xfp/GfB3qoOMXRvgDi8t+UwdXaxfWQq8DnwG3AjcD8wD/oqdFIGho/vVwJvAKb/10vXfA3bR83NiFKrZ7/2W63xgudXxH97ApTZu8av6A0usaZtocfyUGIPMBMZrwCCfs8VymmWA/Jj1kQeGVuB5Y8MGA+Frn9ANWGcr/Kr/DX5GuYApSAnZCX8QktcKqnv9z57pwHZrzq1ZkY841gv9DlVdsRYkC8YllvRKZ+CDmecC41Fnxz+1QMwDo50ncCkwBTjk6AqM+C5Tc19w221Ovb3RywSIhhRfPhf4dqw5//qzMh9B5O81sLVDjDRqP5EDxjXAO36EUOKrozjOCYw88PSytZbYs3bJ+1EmYT27G3jbzjG7C5Dv43egmp+1EWi1fPQChgGfeJnkgSFQpUvSA9lLm8IQGM943GJGe/elRTprpGytKpungCucCUcyPrTqer7GBDNmhsy62ooJCIH1nguYNCg7inwo8McNrLf80LaigBnB380OiDQiDDFK8a2yPmofcIv3IE/a7wfjQFLA0HX/BP9+ImfZIT15yGs60D9ro6Sk3hLQWFuCXZEPMaIDsNHZUwaG4vymoCEM71JzKe17A9hUDxhaVenGbEc1j1kSLO0wonGtcbuXyuhMzWtB8nxcBtxn7HrZdUelVAsMMXcSsNDtQywqQwn7Mf8hiPuv2c8XtZghik/1lRQjFJzuJ+KkBwC3uZLr20gYqt13HcjN/qO26/etVIZbv/B5ZFvk42IrresjOyX7mL9LW7YYEHYvsec5F1HdmYSh39VjHDbxnunC3dFz2umlc8a4CIzQMCmh36NkROf1JQzQY33KU63rK5oaG71H/cGdXq/7E3xkTcqYUeRyPPBLtIhBzJ/O7kpFfYYERx1nPLTFZle1Vk5ihz5R7vCtWT2Cvrf+1gAQSkDdp5g6B/jUSuiHRD8qi3GmWee5wKv5kth/lVfziT5bvlnKbtLyUfAMKzCipa7AiMA4DSmYHjSLFPBxAAAAAElFTkSuQmCC"
·<img data-latex="\frac {1} {2},\frac {1} {4},\frac {1} {8},\frac {1} {8}" data-qs-formula="true" src="data:image/png;base64,iVBORw0KGgoAAAANSUhEUgAAAEMAAAAkCAYAAADSO4eRAAAAAXNSR0IArs4c6QAAA+FJREFUaEPtmWnoTmkYxn9/u+z7mi1LIksmWT5ISZNERFlLdrJLjKXIaLKMRkjKUjN2EvHZVjQZSpYs8XGU+UIkNBjPVfcZj9N5/+d53/d88e+cL2+d9z7Xc5/ruZ7ruZ/7VJBf/zNQkXPxlYGcDE8NaWR0AlYB64GXJaooC4ymwAZgL/C0xDxSMQqR0QEYD/QC2gDTSyAjC4xmlkdvYAAwowQygjHSlDEU+KlEMqIJzAKjB/AbsLgEMqI8UjFyMorwjCxmNQuM1FkN8JFUjFwZuTKSd6RcGbkycmWUbKANgL7AcGAysBl4ANwHPgc4t0KywKgN9LeCSzXGbuAmcAf4NzCPYIw0zwgcr2qE5WQUYaBVY8oD38JXRrXAZ6KwJO/4rjF8MhoBCwIJuWRGFg8fBfQJxHhvh694eGNgfiDGO2BXQmwTYF6xGLln5J6RrJlCytB9Sb4zUNP2+m1WZwSq75uw6sCPwF/AP0UAKI9hwEDX5LkLDAFuubrjAvBfIE4wRiEydOzuAhyxQdX1Uvtvmmv0PAtMwg/7AdgBzC6yOdPPyNjj2n6fgBrWghQZtwPzCMZIIkOzuNap4bzNhsZsCxwFDthvlMdEMzC9qIxMCcevhsB2q2hFZryH2cIqy/YJbb2pjsT6rvW43wNVRazq84x3LwsMksioZeV3S2AJ8MYlqz6iyLgK/GJJ6Nl1FnsFUOLPY0woZoIjSu4+rkDbTmeGk0aWdhH/xbU8DjlF/Oz6saeBOjZRh2OkZoGRSEaS+jTYH8BqJ9vLXkBdQP+NBU64c8zj2MPdgBHANVsmST1MESZVSM6K3+lhaFmIZN07Z0v0LPAogfRyMYLI0LJZAbQzJbyNJSIl6f/fY8rQAWmRI+u4HdrSGrrqfouQgzH81k6dK516ehppywApMekqCyOkzpCbzzIDfZGQgfxkpvnCB+9/KUKyvmjqSSNDY9yLFXNdAb28Ts2vgClud9tiy9f3jGjYsjDSyNBsyDc2uuo0iQg9r28Z2mG0FKJLs6nE97mlpSoxrZcg1c0Btlq8cIQtI1fbQGYe3dOyGe1UONcp8rU3ZtkYlZHRyn04Wmq7hIjQC3aPvfQgYLDtBh+9xJo7t9eHn+hSogstTutdCoh2HqlnjZnoQ+8Z3f/VjXkMuO7dF7H6lrPc+7CVBUZBz6hnzJ9yM/a3JaLaQ0tCrl7slaaMQniTgI5mviJPkydlyI+0y4QUXsEYheoMGaIqTv/SFjvSVZJ/FsmElpqqT6lsk83yk0AM7SZjzFhvuCJQHqI8tHP5/lQZXDBGmmcE5lw1wnIyvHnMycjJSF7WXwCFYiM0cnsOGgAAAABJRU5ErkJggg=="
·<img data-latex="\frac {1} {2},\frac {1} {2},\frac {1} {2},-\frac {1} {2}" data-qs-formula="true" src="data:image/png;base64,iVBORw0KGgoAAAANSUhEUgAAAFcAAAAkCAYAAAD8fqYDAAAAAXNSR0IArs4c6QAAA+tJREFUaEPtmkvIVVUUx3+fL5SIUElNQ0zQECEVwQci6kTEiST4woJSfA18I1o6CAQlFR8ESpiD0iAVhUaBA02JCnHiI0LIgUiCSEpJpGDW/uM6evk459vr7nOvA9lncuHctfb+r99ZZ+3X6SBfbSPQ0baWc8NkuG1MghjcYcAmYBtwP0FHD+BD4C/geIK/XOpqSOw26haNrQruUGAuMBp4A3i/Sbg9gZnAZGA68FkC3LoaonQSDdyxxTJ3CvBRAtxCdx9gH3AuAW7RRl0NiQyjbtHYMtwow0qDDDedXdQzw40iSjfIcNPZRT0z3CiidIMMN51d1DPDjSJKN0iG+yowBpgBLAK2A78A14AnTj2jgJFh8bHWfE8Dl4F7Tv9WaHB21bSZK7bYPLfpXrPDcwIZbhuzIcN9QXC7NdlPWe1tpo26/pLrrf9NhlZq3nRsjZn7GrDKqeIscLHEdjbwjqONf4HdJXavAKsd/jI5D/zktG2F2XxguKOhP4FDsnvZy8IE4DugnwNKZxNtsx5L8Hvm8rLDrcOmtm8VXN3XK/4WoM3hccAum+d6O30dWBJOIm4Cs4BLwOGwP/zI2UArNDi7atrMFVsVXG1Qq77otfjPTiV03PNe2Di/4ZCi1cu68HC+BG4DfYEjwA/AfudAVFeDQ2aSiTu2MrjdgY9Dtn4boF6x7gcDXwNf2G+hal4AdwDYY78aqHRpUJsD7ACKeyvCCu1dYHEYtP4wO2WAjoDeBD4ID+83u98KDUnkHE7e2EoHtF623B0QlqprgAcBQH+DqhF6pwnQg9lqtt8bNGWprrHAN+Z/xu4J6npgYQPEt+34R0vtleG87nOzbYUGB6ckE29s7tmCIBwFNtt5WKFKr4j+U5YK5vUKucWD0KGjAP/d8ICUtRI8AtjbRbh1NSSRdDhVxeaCq1d0QxiMhlimFmCKfpVl+v8rq69legTuoGX5hRKD8QZYdbnsaoUGB6ckk8rYPFOxacBS+37hTkn3qseaFWhRUDYT0MJApeRHKwEaIDtfav9qxcJEtnU1JFFzOHUZWwyuttZUdz8Jq7cysPLXQKQZRFlG6sMJlYFbXYDVG7EM+DSUnX9KAqqrwcEoySQaW1dwB9perGYDAjvI9mcbIU6yDz804j/uJFFtL7Bp10mb0ml/WHvCd822N7DFwP9aEmJdDUnUHE6e2CprrtJ9OXAiZNXv1pnmnSoBAuW5ptoDOWWANfipNqv2ej6NaoUGj84UG1dsVfNcQdCKrPHSlEyfKP3sUKMir9nFxE62ArsxZOvDSBvFAFZHg0Nmkok7tljNTeo9Oz0lkOG2MRMy3Ay3jQTa2PT/w7wmNED9VQ8AAAAASUVORK5CYII="
·<img data-latex="\frac {1} {2},\frac {1} {4},\frac {1} {8},\frac {1} {16}" data-qs-formula="true" src="data:image/png;base64,iVBORw0KGgoAAAANSUhEUgAAAEoAAAAkCAYAAAAuLqxbAAAAAXNSR0IArs4c6QAABLNJREFUaEPtmWnoplMYxn9jl33f18wMkSWylqUkyRKRsWbfsstOEZKdkCVGw2AsifgmeyRLWbPEJyEUIiHr+U33ozOPZznv+/9/mek5X9563vNczznXfd3Luc8UhlHEwJSiWcMkBqIKRdBH1PrAucAlwA+FmPVpk4GxInApcDvw2ZjryF9bBDga+Al4pASvjah1gQOATYE1gCPGIGoyMFaKdWwGbA0cNUGiFgX2AHYAdgVunShRFck7AReOSdRkYkwHbgZOmyBR1ZqWBG4CXhiI6vangaiSeAMMRA1EDTGqSANDMC+iCQai5neilgG2AHYDDgGuAD4EPgD+LtzcZGAsDmwVxaY1lAXiG8A7wB+F66hP2wSYlgroM2JPTwDvAt934fUdYcZcy4L32kBUoU0HosYgaqHCd6ppTbFqfsXo2vrcfeaKWg44uZCs5yOo1qfvBWxeiPFbHHTr05cHTirE+BW4pWHuCsCJhRhd0+6ugvzgeoVsDkRNkCgJ1I02AGx2WctcG3VUIfQ80xYG9gTeBL4dAcB17AJsmxp47wE7Am+luupp4J8RcLo6mhuHm1ojbgTcCHxXx25TlA27DdOLs2NBdjttCR+emnifj7DAauo2wPXAcSM23rYMom5LreC/ADdsW1qi3i5YR19H0+LzYuA84KuEuQ9g23lWCVFa/6KkoqfCir6zJvAgcE/8VjgHRTCVBIOqm6mPZYHrotKX6HrPe5WouNduaPUelgheOrWj78pAPSlYlT+ePevCcFpT/8lnquf1IMZ13gm8AtxRQtRicWRZNUX804Gf00bsXUvUS8DVAaIatYbHmxcBN6VV8uGcAxOJZqH9W1q5Hnht8HtkMtvlpOhyM5OSrkz9+8eAJcKI99UI78JoI8oevEq1D/9JnzpLg7kLeQA4P/rMFa5W8b/9gDkNH5wK7A68HK7X1PN2DapJN3O+Vq6GrqYBfPZkuL1ns48bDNKG0UbUwRGb9BLPeWsF7qtNpJUQpSueHUAq6JcakAr0//trivJAe2oi8mHAA3Lf5YAWlqx7a/irJ1Wfk1RnPJGMM0PBTftpw2hyPa+/xJoBPJsuG6wjNYgK/h9ZJUSZdY6NYP5Nw+qMX8dEHPo9+18l6SrPhOr6iPIb79cKWbOQm9G9fwQOTVn4qggJeYyqPtuE0aYoidoZODIp6+sA8FllGAvi/0YfUVrROHVZqtqbSPJ9fdxMqHtVw4+5KYOi1XNf403ZH5+C7jUxXxyxTSqmbRNL9UxX3Dup94S4wKy+2YSRh4j69ZQ4Job8zlKitmu6nusiarXo2ZjNJMnN28fJCdk+LhPtE/2ZEbVyykpeWuabOCWym/FF5VQZUtVdEAH9o+wdn9+QvvlQzRUk3bvGs7JL2TaMLqJ0Uw3jjfEXmaJMYpYLGrhXUUuFxR5Nlv4yZltb6WZmn1FHn6La8Iwf60UikFgNqxKMf8aS0qKzKUZZDigCa8XnIjObcU1a1mnzjCZFVcHbSjwflgleR1t3jDJ0X6tyO4qXhzo+LQQw6+0bQf61qJxdhxk2j4ddcF0dzXUiUVi8WqGrdGNf7h1zsftiVOF+FvxpA1GFNh6IGogqZKBw2r975Do0+ZCz2AAAAABJRU5ErkJggg=="
设离散型随机变量的概率分布为<img data-latex="P(X=k)=\frac {k+1} {10}" data-qs-formula="true" src="data:image/png;base64,iVBORw0KGgoAAAANSUhEUgAAAJgAAAAkCAYAAAB1yvMvAAAAAXNSR0IArs4c6QAACGJJREFUeF7tnAeoLdUVhr+nxoqG2BWiJvYSFXuMLRAFe8HeG5bYW2I0dixR7DGxY2/YK0rEhqCioCaWYBdRLIk1xBKTzCd7w7xx5szMOXPmnPveDFze492ZPWuv/a+1/vXvPW8S3dV5YIgemDTEsbuhOw/QAWzKBsE0wHLAIcD0wF7AZ21OuQNYm94ezbsE1mnAF8AJwLcNmiF+NgCWAs7IG7cDWIPeHtOh5gSuBq4Brm3QxrWAtYFfAI8Ap44DwGYE/hN+Gpzr2A41DvNdFrgO2D3JNk9V9NRsoZxeBHxe8swxYT1HDrCfAysCF05FAJsH2Be4APiw4uI2fds2wYadE5C9XXHwOYATk3X6PfDxRADYksCOCdE8BfhXxUlOKbeNcu5SoOOABYEDgaWB1YGfAWanJwqc3BrAfgoYARq1UWLkP4ErgA+CYbMCy4c0emVSkx8CvsoYbbo9GfhTMtZLPVCzErAZsEnoeHzHf8NzN4e/+7iZ8FxgZeAZ4A3g4WBXG+D9FXBU6M6c68bBjqKpucg7ADMBlyYL/r8WI+eH4Z3PAY8CZtQ3Adfq18Fveea0BrD4cgmdRE7U2/L+O2WVDvwlcHkCttuBozNZSuc6sbMrOneVMM4nwFbJzws5HjDdO662CNo2F01zZg4gXyTY8W4JaH4EnJmA7A/A31sE2OLAjUngPhuCX5IvBy67WgfY3oE77RNAljUwtsJ7ApsDD4YbdOw5yYKcXgCUvInOAvwxibRdAce7LHOTJeewAOT3yzw1pN9bciTOTwJHJhnt6wrv2SMJMjNK1UCrMGTpLesClyTZ9jZguh5VZENgmdRoZls7xGxF+ltSOe7JvHVgkm8nZPSZUn2pqTbv8kUSQ8tH7ChsYeVeh2ayXplnXAzLiY7x75Fomgl9x1ktZ4KsvTGjFwVc3vzkP8cmZH8/4KMyBzT0ezO8a7ZbKOVbhKA1Q72eBOk3Be9pNYPNH/QT+da2CWBezTEqDULBZJRaOi2Xdk+W1jrXT4Drk7K7QOBlttdzha7GLrQXl6vznn7vdeEULdfrQZSzY+s/M/OfazzTr30+F8v4e8HW3wSybzWR62pLUeZtFWBKC3cBfwnRl6eLRBB67/rA40nW06G252aioqxX5MBpQ/djVjwpZFC7oTsCFxzE8YM+a/kwgOQ38sAy/hXfFzs6F7xuwPVj87yBzNsQ3RuaIqmFCUJe9tceg1YBmDRhsaCXOdTFIfDfSY9bRcmXUNt1GLH+5BFqU+8tISqMFJsAQSfAfpdkvpf78FAk+3aTcp37Q8lsm9BnTY/8ywWKDY/ZdevQTS8KnFege+nLJZLtGgOnyS2bPtzb85EqAKv0zjKARfKuIy2PIj97WcaULuQVBySiXiTeRrjpWP3lrUrWTH5Tmuz/Nux1jRpcWiivvC/plI8ImUjAbR8ItNnboJKv5vlKCca9u2wn3od7hvqIDcHCwGsVu85CY8oAFvexfNmWwPOpkeyI1gikXp3KFJnWoVwII9Uy8o8+3KFtEuLzc8h+leHsitTf5Id1L3Ujs3WermZH7cauYLLcuAVjyXMz2TIuqbYxyZMj9IkZfaeMQj4sW+vOu/H7ywDmPpbgUTu5KdMJShAl32oseQsxKMBcKCWPFYKYm5Y/GndExQFjM6O4bGaW5Kv/VZVLBvVJFTM9ojMOlyJ56XkwVfwbQvqXIH5Zw/JBnKkMoEKuJHFQIPryGvlddqeghkkD3xqbGfU9G5nja+4xDuKTqsabFCzDo7zEjDsGPQFmJ2cHZ0qvo/fEidlRqvtYQuqUyKyQWkXZb8uZqyXbZg+Ekmj3uGkIQJug9O5GkT0C7OCgRX3altGjfE+vEhn3sXRK2X5b3hwk+ar4Ev887SzvGYVUtTN51yvhhjTZ7wfoTfo3zb/MYGYLo1UOZoYta0Lko2tOAJLfmM96Acx2Wt5l9qmj90TjbHUl/pLldHNQZLzgkpS7a5AVUqMMklX2ezmiaeIcO+pVQ9doZ+wc3d+zHNgZKj3sEvyWl6EE6NyhMqRtb9rWOgBZKHTE6aM5MyRNynahcXEeBpICd+3DBL0AZkutsKmoWHW/LT2xSIjVr+4smbFZynJcJKTOB1yVyAMu7qjIfuRfdodRZogAezH4yK5b3mo2y+pcEaBqenkSRh1QNHGv8pKB6xaW/k13tpZ+QeXxKudhV+ypGLFQ6yoCWFpJNyJd3H4uDdN4M1NR+VBxVi9zb6xIyLUz8ndG2ajIftzRUKKIjo7lW9sNEKNeYThu9qd9JvjcJvK+Khm9H3/380xWOnGnwr1e56CC4CX3lIt7AKHsAOJkNmQB9uNwRCZuA7iw6jueu5LcPl1zBkaHnZ/ENm3YD8J71JLcd3SSZga7RqM7Hf3apKi5DuA2izb552PhREPttF1zDvF2Txx43MaA0x/xUkbx1Kq7FYrNRUdibFY8HWL2a8vmKlPNAsxdCc/w2yHHA4nyaQNbaabWcaMyHayKgb3usZb7RcvdBVE96PgT5flYEdQMbx0zo7MAE0wGyf4ZgGX/rdI0hg0wjfCkqntwbvdUaeUrGT7BbnLRDg/ZvFaJaWGeEx5g7mt5hMfotcxObZfz94ycJ4L9GbdrwgNMh0qGdbLf5o36LFebC2yF8JCAl3pZmU7Wpm3xXROag6UdNnvQ0wTZuJWJYS2sDYBNjPrdd3tzY3jldZF2yR6XjnKK9yhV2UXW2ZUp3YscQ390JjXsgbwTHmZdP21zq8/AUAXweLVHkWpl4TZIfsP+6IZryAOeOPY/RvGLMPU79Tm/4PLDDmUkv6VQTjFjeXpEJb/sK+/vmdYBrKHV6obJ90AHsA4ZQ/VAB7ChurcbvANYh4GheuD/mKPvNJiPzwUAAAAASUVORK5CYII=" style="vertical-align: middle;">，<img data-latex="k=0,1,2,3" data-qs-formula="true" src="data:image/png;base64,iVBORw0KGgoAAAANSUhEUgAAAGMAAAAZCAYAAAAlgpAyAAAAAXNSR0IArs4c6QAABXpJREFUaEPtmWeIbEUQhb9nFjOiGH6omDFgRoyoqAjmZ074Q8wBc8KAGXPWJyr6zIoYUVQEIwZQUEExYEBRxADmHPqT7uFue+9M351Zdhj2wjKwc7u7uk7VqVM105h6hsYD04bGkilDmAJjiIKgCYxVgQsAP5cCdgAeHiK7R9KUbpnhd2cAewG7AG9Okge0YxNgc+AVYBlgQeA64NtCm9xjOeB04Bzg3cJ1cwI7AqsAcwPrAPcDtwHfFe6xNHBAOPtv4NewfjXgDeAm4KvqHt3AWAC4Mb7sZqWHF9pY9Jr27QlsAJwI/BRXbQocAhwVPr/sstP6AcBtgMWBhYDlgd0LwRAIz3geeC2esRhwITA/cFCPs12ydli/BXBVsP+XuIegngusCewPfJLs7wbGSsC9IRoeBU4Lf38VuW+wLxlVBsQpwKuVrXWUTvkQuDJk8D8Fx+4dwDy+BRg6cVHgrmzv1YG7gceAU4HfGs6eAzgPWCIG0qeV98z0Z4FjgMtKwNg+oPcQsAdwT8FlJ+KVnYEjAB35eXaAkSmF7At8XXB4GzB05AmRjjqRW4lsHSjdSOH598mUWSNY3sH33q7YuCHwQgyy83uBYcaI+n6TWC+8zNmRWupo0mC5uIV9bcCQ0qwL1iap5IMMbJniLGAj4MWCQMhf0a9Xh9qxE/B0LzBSvZi3EnnzBHR3i4VoBeCWELHvj8OQ0iVya0rhoyucm9an6Cp1SBswPFuKWbcGjCRsDgy1ZLtKPSm9l34UiFli1n/fC4wVIzXJi0aB4EgLM0PELBt48Iagam4FOilWakmL9xYOWXFHcMbHQTx0A6OURtuA0c3M+YBroigwwr9ocScBkLLMCOvFGIprKuBbBgXzZEjPfYAHI4IWMherMA4DDg1y87mKIbPHAqnSafv8EQtydb9SMLRR0Ho9gwJjvegTZb/iokQ8WLCtMa7Vh6qrMbJW45vAODkCoAxUnj0RVMg7vW474O+HEQwlrY78MRb4JLXbXH3JWOtUh9dX6bcOjJSGavSXY5P0XpvTBvTusIExG3BspOmTWjScde5I8liqvwT4sykz7FTV0UoxtbDSUcoSxdKOdxB4TGYBz+1PzacULGv064ckkMY0oXWZUa0XcrFppcx7vUeTMwgAqnskabtW7DO+yQ6wBsjbpaOa8dYMfbQZsHWUs6XUpNqbAdwcuv8rsqY5BZqiqKMG68BQudipJtmWFtoNeyGd4ojipah0ko8GXcDd1/MUCnXNlXZuNUFNXxV3s0EwLqqMY/zeqJ4LeKshClPTbPN4aQZGKgXSVWc8k4ORXlqkcskEhhyeBl4qKgd1Pww6HbL9DAD7GZu/TnMUeDbZ6cxoosYhmrJyzAgjPM2Wkok6UVHTNEB1oGkwCWI+MnHweF8+UsnBcFx+Z5yOWqR+D46QLqQD5zRGo42QB1l8JvpJXK00tHgminCCe3BUfGlQaK0TuM/i/3Pp2ERT3s+B43HxUyclIIxq53M5EGaEY44z45im7mxt3zXSvH1Zst2mz7maaw6vNs45GGvE4i1NPVLxtCA5HjElpSMjpZQ7+wXMRknny9nPxEBwXKGgqDpcjn48Zo309VSkEp1mJkkban0Hn1KsRfj2SB92+vK3tdEeSr/oQKO/6bHHEMSfw1l1ZyeB5MBVqnXQKsVLTQqj/43hR+mXPkGTxx1NG+0ljWBytP2D1LFt5PdcLPQKqH7O7uw9SmCkS5kB0oqZ0eZRbh4ZhoOX91ELx3v2f3aOGhhmhLVF3v+oDRKRPjYOtfHawhFHvn0/Z48kGPKx9cWRRZsfw+yuLeAPFP4KWIfzeM8eSZpSeis8LMbdfoqtc+T0MDL3ByUnDyWDv3yPfs7u7PUvv/BHKYRNf/EAAAAASUVORK5CYII=" style="vertical-align: middle;">，则<img data-latex="E(X)" data-qs-formula="true" src="data:image/png;base64,iVBORw0KGgoAAAANSUhEUgAAAD0AAAAZCAYAAACCXybJAAAAAXNSR0IArs4c6QAABMdJREFUWEe9mHfIr2MYxz/HOmYcMzKirJRkR3YUCkd0jqyMSPbIKiuy98gI59gzQhGK/CGjSLILiche2fP+nK77132envm+vb+7ns573vd+rnHf1/X9fq9nGuNdCwE+v0+h20WBv+OpdTNtCp1XTa8AHA3cCHw5hX5XSvaPAm5I/r6u8zOupJcAzgTuBt6dwoSz6fWBA4ALgV+q/rqSXgvYB9gU2Bf4DpgLfFUxpJPtgTXi78cUzvRxOPAbcA/wX0PSKwL7AzsCWwFvAssBD6d/rwO+j/fcdzFwSHo+SfG9Fc8twEexR5/aWgy4teqzK+kc37bAC2HgeODXmsCXAq4E/gFOjCTdtm76+TTg5CLwtsueAdwGzAQOA26v2bxe7LkGeKShf7VzRUr8EuD90kbfpE3ChE4CrmqJeBawDnB+ceK++2ME2beyTdYbsqrKqvF9W0X7j8VFtNnUztIR86jC+iRtiZjokcAuwLMtXrYGNi8OZnngWuC86ml3ZL8B8BCwDLAX8GrsF/k9xE+BB1paJZvXztkBoN/kX/ZJepXoRcvFm5yvVCrB7wzYc/auy0M4Im7r577XDEwHLk0Ycly0hYe+YBy8uHJ/j4R1Z8tdH4zx8pCkt0zA8gzwdACSpZqX5aOxt+MXe6Y9nwGvxf+tjpXjppsArOksdgIeBV4BDg6gXDXaTB7us7zUc9JhfZHiuHlI0gZ+Uzr9ixJInRVAlU/x9CjlUekUkXgz9t57wJ19IqzsKQFNZDbwy+ooqMP2QakyBL5R7F3lvUjQg300O/pIH763H7Bx8O+fNY4zFjyZ9j0+gaR9JQOaoHVoUOZQU3skTNitZJSupFVR9wJbpOepgnLWDFCz7JpuUY61t73tF4dGGvs3AR4Mvi0BbYg5ceUM4MAcf1fSOn0CeL18KYHM4sDlQUO5f6uBTDZp5aT8rh1L1MOTBdQBQ5ZJW9qKlW9zmbYZcKPSsdrPlq6nZ69/HgYWSK2g2M/CZTJJm/C5QXfLRpW9Ey318ZCMg0F6J52ByOTUsZmG9LkksF1wdu5n0Xb1JEXnRFCKAgXG1QPLuyo+SkBTzqrWhixv+oSSedrKW2d3hcJSf6uFm5a86uHckegl30QGsucLAOwKVvFxbGhq6SrTXAY043FSG8L5Vus2fYFswxD7H0Y/19FSTsKBZNeYasqes6wcTkYc2ZK1CStz5fn7KuJD4PR3VtJQQJNyFUxZGs+jnqYl1EsVqiH5uI6WfFeEF9ScX7NczDZVcCJ/2/sZW6TAJvFhqykyPMQhgJYpV4GjbJ23mpIu+7mJlnzXG7gglfYfNYOB9mu1b+WUbQ2l6u5RUbWDfxoudgCeC4XmAfUBNLW/Hy08qFF7VpNeLeZmJyXnZ5FTYKrqbZHZPlGi2l9yoFVRXYKSlSKgVavAlvBA1wY2AxaOAGWKHwpDMoI97fz8E/BXjJIvhYbIM3RdxTr8CH6Kq9HHhC6e7gKePn/fG9hoghzbx37TntwSb8TMPdo3jqRlAScm+75tQptMgnXv+vHilKQbTq1+vBhH0gYkp/v4zarvhDSZQ5AJ/Cbn1x6f+da4ktaPA4ur7yw80aQ7fY0raRPw9BU5H4SWn2hSXe85+ckqipt/6zb/D/zRBymg4DQ0AAAAAElFTkSuQmCC" style="vertical-align: middle;">＝（ B ）。
·1.8
·2
·2.2
·2.4

·正确
·错误

·正确
·错误
设<img data-latex="X\sim N(0,1)" data-qs-formula="true" src="data:image/png;base64,iVBORw0KGgoAAAANSUhEUgAAAHEAAAAZCAYAAAAG2cHnAAAAAXNSR0IArs4c6QAABvhJREFUaEPtmmWIPlUUxn9/RcUO7EBFVOwPimKjiKAoit2d2N2N3YXd8UFRRLELW1HswMRGUOxAUXR+y7kvs+Odd2Z2X5f1z94vu/u+d87cOc85z3nOmZ3ExOrigRmBP4Dfu1w0ir2TgJmBH4C/6+y4aWK188DGwErF1hPHEERPtgWwFHBa3X0nQGwH4GrALsChwLftLhnYLjE6JKydm8vIJhBnBQ4AVgFWAD4HpgdeAk4B3gzj7juv+Hsz4C/gPeBj4HrgvoE9TjtDnnM7YElg5cLxPwO7Zs7hmQVlXWAGYJbi92eBayp75wQuAS4Gnmp3hIHvmg24FLgaeLRqvQnEtF/gro3U9iH3DLDK9hYqHHcb8DhwKvDjwB+lm8EdACN39nj4faKeVa2sGgFotD+ducVhwFyAP3N1aS1gW+CV4n7WTKnvzFKAtzn1YsBZwI3AnTUXbAhsD+weNbK3rS2IXmB0Xwa8W2TaNpFtydA0cXAzNZvybZ5kwHt05HfAjmFXR7+cucfaEZz7Z0CeLwLgDOCJzLVbhlP3KvzzQXwv9Z5e1K+jaoIimVkxzuY9pgbWAzbtA6LZaCKZRPeUz9IFRKPl1sLA8sB+QTHaSpw9T+GEo8e46NfhLjVK79LgEQFS+czl6w4q9vwGXJ4xplMFf+dq9APzAjeH071PWvrj7MLe3MFYv7QIzk2AOxpA1MxxYXffMit0ATEdTtqRNi30vwLSlFR6zDgB0IddLmq5AElDMsiTQUdlYWIGXBTP81jF2T6v4HxTOOyEDBDaPR/YA6heK5UfH/d7boAgyhr6WftflKOmxT16W9YM3vYDDRltGxUPamSMtWrrd24zSLoyCxODLBhnvr90oec3a44sOyW+t5aaaVKYQVtdJ0XmmKmvVb6UGq1vBrw/m1bbTDRZtGeb0wucLpnoQcoC5yHg+3CUSnQ8LR38Vji/zCDW67JAUdRY381Ym/jyWhy4KmrbM5mHM7stLQbMZ5XvVcU3AVdEkDT5pi2Ilokbgnp7wdEVRA+TBI7p7O+2G+NpqRClOVuClCHSkA/9VUWUKUjcbzZWl0D4ueWimmlOUWyfFCX9QDTrrcVNqy2I04XQUgn3zjwSEJcNgaOUrhMLTYeeI7jdw88UKu6C6IFqx0vAhbHn7j43MIOOjeyynrlUdmbG+qEIBdRn954PFJOYMsUm055Nms2B1BbEh4G9m5wBtAVRUzLAn+Xg6AqizjgnmuPNoym2d+lSD7VxJbB0ZMfXBfVpy8g3e6TC3GzSKPQ661M/EK1HNvBSZHlZt7WfRNm00Q4pWnLlYDyD6HP1gqMLiDrfyL23UKafRmQbkarUYX1LQ+TZrErDUtk7sXfKsKNDb48MqAK5RGSiNa1Kb+Vbmj1fZgSFivWWoE9Fmcp6twDb36trsgOx2sybFWmC4yiobhpSdUzKJilM5VddDnvNdOlNMGzWXQoqG26DRvBzTnef9q2HnunFinHbCUdXAqf8/6QIxEVq2gcvNaOV81tnhEuitbEWNum+jhIN5qHVJhNTM++s8eQS1SWB46Riq5jkNCThkBDQkUp/Jz+55dsCgZT3rV2JbheI6UhuNJbs2EaYzYdHf1e1b29n8L1d9HAfAnf1oWbpXeaRhqsBoV1p3/bCclLtBVONc1o0yBYj1WJnvK2FTQJw/nB8meIExAnOGh0EjteYUUaRSrFuLRw0J6BJ+Dhwf6EhSlShG0R/lhNI5TO/2hB8Bo1iyMCtNvMeQ8HjMMByUhVGsoXD9RzAuUdoK2xS76o26M1YmzLR2WC/Zt4xkA/pm4quAqcpa0fyvcHxU80ILdlLZ3bM5TjN/bll63Ed8EiNvTR2c+BvgKUlbdsfTvUfjN2s6wbOwWV2qANRoSGNKEJ8Y5Frdj10muBYi7oKnJGA1O8aZ7c6vW7Ckq5NjbgiJzdOK98jO6ssbTDIzTpHb+/H56vHywApPVG/kxbrtG9D9FOVnttmotlvTTdhUvv0r5rouzh7v0WLyYCU5ljqwUDeOpKWILtvpyITpyjVyddjmjCW7xBtVYzMdeIcDpx1ngPwjzKoK5IcdlsPzcZ+yyBVYOm43qyydIFJYDujU58P5et5rFfSdTVwFFIyl8Gjj00SM97J0TIFRb8RCSM7OC1KgaGdNHnyXzXKmd9K2Aw6Y/5P9gTcDLKtyqnpts8iAA5HBEvwrJddlzNgqdSgGvZKrakmdr3R5Lg/TXmkTLNgNMu2RbYblkktDVrvFTaCOEy0TYDY7MHUIzuvdPg8mmWNlWa7DEe8n4MOgRfA9PK5d44JENtBksaNiqZ+fWo/awJxYPSwXTK68d4TILYD0V32yip2XyI71uuyFC8OMOw7uwSBAtIZsGo29+8hQ2f4B9UBoykpmEXcAAAAAElFTkSuQmCC" style="vertical-align: middle;">，<img data-latex="\varnothing (x)" data-qs-formula="true" src="data:image/png;base64,iVBORw0KGgoAAAANSUhEUgAAADQAAAAZCAYAAAB+Sg0DAAAAAXNSR0IArs4c6QAABEdJREFUWEe9l1nIVVUYhh+T5iAwghDCBjEIGiglDMKiiygvIiUbaDKFCocUbZ4LoszMHKhoUivEoAGriy4SbKCoiwYaKCqavJFKItMMxdZz+NZhu937nP17zn/W1f+fvda3vvcb3u9dIxjcOhA4APi7hysPibPb6myM6MH4UI4eA9wGPAJ8P5SDpb2jgAeA1cDHVXYGAUgnFgPPAe/3ACYfHQvcA9xXFZzhBqR9L98OLEp/7+4DIE1cDkwC5qbM7yjaHG5AE4E7gOuATX0Co5lDgaeA9cDLgwJksOyZv6Lu+4inZeoKYDIwE/gnG2+SoZOA64GzUzRODAe/Al4DngW2RMTuAmx+L9gKjAGejpL7sN9ogHHAE8CdQNt+J0Cm9Xbg0mCVtdGEUu/JUb/jgYcD7LHx2+fh/NQAdyXw+zAA0g/L7gvgsW4ZcmbYxBOAG4DsZLlcrwpjRsg++a2wQRY6KrLbLzIox+VW4IS4+z8/1mXoauDm2FhHtadEyg+OEvPMj3Fjjt63wEMdsjMSuBawrF37B4mcDpyffHCAjgbuB36qsDMtzttPrSqoAuTceAH4qEMznxcN/yawHHimtP/w1E+rgLdTlp6sAeTdC+Lbo8nOEcCLwC7g50T1t6T+vDEFa2HMnHZZFewJWha9DPi1DpBltjI1/3zgg5IzOnFJ+u1eYEXss5xMvf00PaTN0Snqr0R2Xq0BJKXryE0xSyxzSUQnzdo7cYf++P8nFXa0sTRlZ3b+XpWhKeGgTd1CHcvyEKQsZlR0NPeGZ4zkxTFvmgCSFT8D3gj79pvEs18MziZzS0DLgoxaTNcUkIynAxcAc4CNpWjtC6BywHXOUn+v2ORd2LERIFNsOc0Lfs9a7PgSLRfvsmzOKJRcjrb9VVdyZV+ddc4VWbWu76qC4PCelZm4GykYMY3/G3VapOVsvIpEMim8W5wRHaKdWfEswLnVdBDv1R6daNvG3xklYH/8WeFQZiqHr458U9hjtDeHUuhSOS1VoSZTdbQpOAhCsvHJULWcgxclSr8mFEztHDonGEcQMsyXNWBkKWeEJLGutEcCsXwlkfKD7MyY8jKXDHVuPC8sT0tPspH1LCeJoi5jfj8o+rp1fTlDRVp2thyZpIVplU5fCgaT7U6NHjN6yqPXK54Gyvu7IyDOleISrM8Kg6HtB0MHOljN0B+JYWekd9RhwOM1z45c1mrKNdl4GZAT2p5x0OWI+5tR00EfVwrPr1P034qhaplULXvLR50CNlNz3qeIFewvoQ42pJmkqshvJ9XzD0ngPh+Dtsr+aTHnzPB3dYC61fpQv3uZEkkWammtPi7HiFmSYdtascnzoRcf1GGSg3quKXM1ue84YElIok+LB4YbkHcplSQZddkez+UmnteQkdmRaGyNPZT8IACVRWivTwkDJHvKrHsFaBCADLIUbD9J/yrwfV0+LC+Mcms/u4vG/gfF++4aJHRs3AAAAABJRU5ErkJggg==" style="vertical-align: middle;">是<img data-latex="X" data-qs-formula="true" src="data:image/png;base64,iVBORw0KGgoAAAANSUhEUgAAABoAAAAZCAYAAAAv3j5gAAAAAXNSR0IArs4c6QAAAbtJREFUSEvN1c+rTWEUxvHPYaBQYkQMrgETZcLIgD/BxK9uSEoG90oxUGRCBvIjA2XCTdQd3DISxcTIzEhSbgY3MZUMFCX2qrXr7WSfffY5t5NdZ7Db71nPu9b6rmf1TOjpTUjHfyO0HmexB7vxGWvwBlfxLisS525X7wfwG4tYwkM8jzPDZhTB53AID3A6A5aVn8ICXuEavpcfhxWK/xzFPXyobjydt65jrcL1zPgW/vT3vovQdsxjF87gbgaLGOexCRfx81+AdRGKszcyaJToJH5gpupFlO1Sk0iXHtWX3IdH+XIcG7Efs/g6aFS6ZBRxSihe4hsuJGEDR7KrUAnFlwQkUG99RhHamVDs6INiWTPagJvVby0O5jAea+tPVxhC5A6eVcR9wmOsS/qettVu2NL1D+TqwinuJ+K/xqWuHsjwsyvFrNRO8RFH0jEatdoyqkW2JMbl1G9OKPYOA0Wb0OGWgbycWYZDD4SiSWhlTvupdOrXDTWpnSJ6FpbUCEW/UOycMMxt2JoW86Ky/HPVinhfiMVF4tyJKqMVRd/e4km9g0ZdE20EL+vAjizWBsPIgcdZfGOJTiyjvxSDTxoAWbZCAAAAAElFTkSuQmCC" style="vertical-align: middle;">的分布函数，则下列式子成立的是（ ）
····<img src="https://u.qsxt.info/degree/school_4595/39538220_20240114114938447_382.jpg"
下列关于中心极限定理的说法中,正确的是( )。
·它揭示了在一定条件下大量随机变量的平均值近似服从正态分布的规律
·它适用于任何分布的数据
·它说明当样本量足够大时,样本均值的分布近似服从正态分布
·它指出,只要样本量足够大,无论总体分布如何,样本均值的分布总是近似服从正态分布
下列关于点估计的说法中,正确的是( )。
·点估计是用样本统计量来估计总体参数的方法
·点估计的结果是一个具体的数值,而不是一个区间
·点估计的精度可以用置信区间来衡量
·点估计是无偏估计的充分必要条件是估计量的期望等于被估计的总体参数
下列关于假设检验的说法中,正确的是( )。
·假设检验的基本思想是小概率事件在一次试验中几乎不可能发生
·在假设检验中,原假设和备择假设的地位是相同的,可以随意设定
·显著性水平α是指在原假设为真时拒绝原假设的概率
·如果检验统计量的观测值落在拒绝域内,则拒绝原假设,否则接受原假设
下列关于回归分析的说法中,正确的是( )。
·回归分析是研究自变量和因变量之间关系的一种方法
·简单线性回归模型是指一个自变量和一个因变量之间的线性关系模型
·相关分析是研究变量之间是否存在某种关联的一种方法,但它不能指明变量之间关系的具体形式
·在多元线性回归模型中,各自变量对因变量的影响是相互独立的,一个自变量的变化不会引起其他自变量的变化。

·<img data-latex="\frac {{π}^{2}} {6}" data-qs-formula="true" src="data:image/png;base64,iVBORw0KGgoAAAANSUhEUgAAABgAAAAmCAYAAADeB1slAAAAAXNSR0IArs4c6QAAAhJJREFUSEvV1kuoTVEcx/HPLYW8MqAURspUyZUkMwZGJiKJ8kgolLlXMfAoA2VAeZaYKCHJTFGMMEJGypVSlFee619rZ9/Y5+5t73tj1+50Tuv8v+v3f/cZ5qdvmO375wHjsAYDWIDDeF32SlsFCzEWt7EzvW9xqkvAUszFIazATBzsElDYGo39uIQHXQPCzSuz0Yv40TVgEabgenr7cRdfCkivIEfwNmJZRa2cxyPswmOMwXOcraNgVEq3rXiGe9iebnkcm3ASL+sWaJWCyO/peIJ5KQ3DDecy6ADetwWUXbgDD/EC67AXn7oCTMORlBm7MTVXbRTUx64A6zE/V+mcnOur8KoLwEScSD3mJs5gdm4DoeB+F4C6Nnqea9vshrzEiALGD3mdZge+40NZwSSsbWaj5+mo+EGADm3/MjWiMaijYAK25VYxORXhjdyeK//bREE0wBiHV3Erj8ctuborm18TwGoszm0jDIaSGDDx+a5KQl1AZFhkxRVcqOPLOhOtbGcWYoKdznvP19RlIx6X8bkXsK6C2H/uYF/2+be0bG1Oi1YU51HE9z8+TQCRMcvzkhXGAnosbxQxWlsBolWH7yOgMaMLQECXlH77DVJXQRHkiMG1EiCmXeymT9sqiItsSANnRp7J0chi8MQ+tKdXoOsqiAsWe1KsiTGTo5JjlXnTRRY1Sf1BZ5so+CvI/w/4Cb8xWSccHEL/AAAAAElFTkSuQmCC"
·<img data-latex="\frac {{π}^{2}} {5}" data-qs-formula="true" src="data:image/png;base64,iVBORw0KGgoAAAANSUhEUgAAABgAAAAmCAYAAADeB1slAAAAAXNSR0IArs4c6QAAAfFJREFUSEvV1kvoTVEUx/HPX/KIGFFKBiYMlbwSUwNFJvLIo8TEACVTeUThP6AURXkNJKZKMaaQwoTkFSEj8irPvWr/ueSeR+fcf5w63cHdZ333b++11m/16fHT1+P4/nnAKKzCS8zBAbzuPJWmCuZiJK5gS3rf4HibgAWYjv1YiknY2yZgINZw7MI53GgbEMe8LAc9i+9tA+ZhHC6mdyau4vMApOiS4/LWY2GXWjmDO9iKuxiBhzhVRcHQlG4b8QDXsCnt8jA24BheVC3QbgoivyfiPmakNIxjOJ1Be/C+KaDzCDfjNp5hLXbgU1uACehPmbEd43PVRkF9bAuwDrNylU7Lub4cr9oAjMGR1GMu4SSm5DYQCq63Aagao3Bd02ZXuolBBYwu3U69Bd/woVPBWKypF6NwdVT8b4AWY/8KNah3UKYgCmwqDuV2HJ32MS4UfVhHQQB2p3Y8GbdwNBfelzYBj3L7LlP78/+6CnoKWIlhyeWe5+09wb0yKXUULM6A8/k3xpPL2Yu7cuoA/gyyKDneimyjb7sRqgKGpOEqbPRdx1gSU93BPLKEd//1qQqYjROIe7iZI83HzjRJrMbTpoCwzpgo9mW7jKljW/bmUPG1KSC+D8tckhWEu4Uvx6Bb6M9Vj6gsG3uSRZWg/7+CHyEGVCed3bPXAAAAAElFTkSuQmCC"
·<img data-latex="\frac {{π}^{2}} {4}" data-qs-formula="true" src="data:image/png;base64,iVBORw0KGgoAAAANSUhEUgAAABgAAAAmCAYAAADeB1slAAAAAXNSR0IArs4c6QAAAdBJREFUSEvt1suLzWEcx/HXZGrIuGyI0thRSikhyU5Z2EpGaZRLygJlSZKwYJaKsHBZyB+gJBslamSBlWQlQ25ZuBTh+dYz/EbO+Z3LM5OFU7/O4vf8vu/n8733mOBfzwTb988DpmMrXmI1TuF11SvdKliDabiF/en5gAslAeuxHCexCQM4URIwZqsPR3EN90sDws2bs9Gr+FEasBZzcD09K3EXX8cgzYIcwduJDQ1q5Qoe4QAeYyqe4VIrCnpTuu3BU9zD3nTL09iF8xhttUAbKYj8XoAnWJHSMNxwOYOO42O3gKoL9+EhnmMbjuBLKcB8DKfMOIy5uWqjoD6XAmzHqlyly3KuD+JVCcBMnEk95gYuYnFuA6FgpASgVRtNz3Xb7GovMamA/trrtHfgOz5VFczCUHs2mp6Oih8HKGj7t6lJjUE7ChZiEW7WfdSJgphex/D2z/H4N1gngHU4m9v2uPlbAjAvtfAtqYXE//vSCqaklr0Dt9ME24hvpQGxnixBjMqDpQHRWXfjXHbNoZKASIRwyQvcyYEsCgjfL8XsSpZEoCMGsWjFRvGmUT10kqZhq6iC6uVm5BEai8C7HJMHzbaMThXUdYhf7/8Dal31E8FJTieB9dMMAAAAAElFTkSuQmCC"
·<img data-latex="\frac {{π}^{2}} {3}" data-qs-formula="true" src="data:image/png;base64,iVBORw0KGgoAAAANSUhEUgAAABgAAAAmCAYAAADeB1slAAAAAXNSR0IArs4c6QAAAgNJREFUSEvt1kvoTVEUx/HPPwoRAyElr5Ih5ZVkTBlISiRRYkIhygBJ/2LgMSClPMqrZKBMFKUYiGKEkWQkjyQZeJTnXrVvrlv3nnO7+//PwKkzuvuu71lrr9/6rT4D/PQNcHz/PGAk1uENFuII3jVXpdcMFmEEbmNHej/ibEnAEszBYazCZBwqCWjEGoZ+XMWj0oAo8+oc9Ap+lQYsxjjcSO983Me3BqTTJcflbcKyNlq5hCfYhacYjhe4UCeDoandtuA5HmBb+sqT2IwzeF1XoO0yiP6ehGeYl9owynAxgw7iU6+A5hJux2O8xAYcwNdSgIk4mjpjP8Zn1YagvpQCbMSCrNLZudfX4G0JwGicSjPmJs5jZh4DkcHDEoC6MTqe63XYVX7EoAJGVX5Odwd+4nNzBmOwvrsYHU+H4v8CFIz9J9Sg3kFVBjMQIouxsTTb5DX86PTHuhmE6HbjeFZxiO5yHtV3SgAiYEzTvbiFsRlwt9WDW2F1M4hz0cYx5L5jSgaE2V8vkUGrSa3F3GSNe6q8oW4GARiS7HB6Djwr38erqs7oBtAca2q20HC3e6VL1Mgm9qBQ/85ODlc3g61pg1iZHS2sM5592YxiN/3QLou6gOWYkFbDc7mLQhcn8rpyrJPY6gJijVmRnG1aVnJs0u9xusqf6wKqmqXt7/8BlaX7DenmVCflF1IFAAAAAElFTkSuQmCC"

·[0.5,1.5]
·(0.5,1.5]
·(0.5,1.5)
·[0.5,1.5)
<img data-latex="E" data-qs-formula="true" src="data:image/png;base64,iVBORw0KGgoAAAANSUhEUgAAABgAAAAZCAYAAAArK+5dAAAAAXNSR0IArs4c6QAAAc5JREFUSEvt1T3ITnEYBvDfS/mKATEoxKAsBoSSjxJlYSGEDJRFiQllIgxiUgbyrZRFBmGySb3voAwGWWSQSEKU8r91vzo9nuec89KTxamzPM9939f/uu7rf50BfX4G+jzfPweYi01YjM14h8t408F8PlZjdv6/D5+ipi2DlXiEC9iPz12knYQz+I4D+DISgGiI5oM4W7O3LZiHY8M1bRiMz6F7sQ4PawCWY0n1EG0AZuAGJiNO+LwGYC2mZ/3PsjYAy/AA97Gn6PuhArAbj4sBnuVvG0vNKwyORKKQ5jxOlgUezSVGfyz1UMrxtherJgZjcCpdsRW3clD0bcNCHCnvtz8FmFZccRNLy3uvWPR9DpqTC9+Fq3Vp0MRgEe5iCDsrABNwGherencDagLYjutd9A/rHs7dvM7Bo4qc4zovYR3A6LwwMWhH1Xrl9BOxKu/EsP5rMKvExaUqkzqA8P21vJmRR09rtB6bjK7gZVuABbhdtH+R+ve0Yobhepyo2Ljxom3AnfR5+L2XFcNpsfBzeNLJspdEVf17WTF6w67Hizxf8Sui6ySambkfiRj5PyWX1pk/U7ECESMfU8Jg+9vTZNO//qL+B2iUsO8S/QAHAVEaFYddbQAAAABJRU5ErkJggg==" style="vertical-align: middle;">的补集可测是<img data-latex="E" data-qs-formula="true" src="data:image/png;base64,iVBORw0KGgoAAAANSUhEUgAAABgAAAAZCAYAAAArK+5dAAAAAXNSR0IArs4c6QAAAc5JREFUSEvt1T3ITnEYBvDfS/mKATEoxKAsBoSSjxJlYSGEDJRFiQllIgxiUgbyrZRFBmGySb3voAwGWWSQSEKU8r91vzo9nuec89KTxamzPM9939f/uu7rf50BfX4G+jzfPweYi01YjM14h8t408F8PlZjdv6/D5+ipi2DlXiEC9iPz12knYQz+I4D+DISgGiI5oM4W7O3LZiHY8M1bRiMz6F7sQ4PawCWY0n1EG0AZuAGJiNO+LwGYC2mZ/3PsjYAy/AA97Gn6PuhArAbj4sBnuVvG0vNKwyORKKQ5jxOlgUezSVGfyz1UMrxtherJgZjcCpdsRW3clD0bcNCHCnvtz8FmFZccRNLy3uvWPR9DpqTC9+Fq3Vp0MRgEe5iCDsrABNwGherencDagLYjutd9A/rHs7dvM7Bo4qc4zovYR3A6LwwMWhH1Xrl9BOxKu/EsP5rMKvExaUqkzqA8P21vJmRR09rtB6bjK7gZVuABbhdtH+R+ve0Yobhepyo2Ljxom3AnfR5+L2XFcNpsfBzeNLJspdEVf17WTF6w67Hizxf8Sui6ySambkfiRj5PyWX1pk/U7ECESMfU8Jg+9vTZNO//qL+B2iUsO8S/QAHAVEaFYddbQAAAABJRU5ErkJggg==" style="vertical-align: middle;">可测的充分条件，不是必要条件。
·正确
·错误
叶果洛夫定理阐述了可测函数列的一致收敛与依测度收敛的关系
·正确
·错误
若E可测集，则的E子集也是可测集
·正确
·错误
可数个开集的交集仍为开集
·正确
·错误
关于叶果洛夫定理下列结论正确的是（ ）
·叶果洛夫定理阐述了可测函数列的几乎处处收敛与依测度收敛的关系
·叶果洛夫定理证明了可测函数列的几乎处处收敛等价于基本上一致收敛
·叶果洛夫定理阐述了可测函数列的一致收敛与依测度收敛的关系
·叶果洛夫定理证明了可测函数列的依测度收敛等价于基本上一致收敛

·[0,1]
··(0,1)
·(0,1]
设<img data-latex="f(x)" data-qs-formula="true" src="data:image/png;base64,iVBORw0KGgoAAAANSUhEUgAAADAAAAAZCAYAAAB3oa15AAAAAXNSR0IArs4c6QAAA+dJREFUWEe1l1eIFVkQhr9xVVwDpjWBPgiKGcQFFcQAiqCYEbMiKC6ru6tiFkyIOeeAvph3lw2K6IMPIiIYUAwPZkUQxZwDYjr/UGfoabpv355758Dhwu0+1fVX/fVXnQJKb5UFtD/m8IkKwGfbkWYKcjCe6WgtYAKwBXiUwzfquPO/ApucvSdRdkoDQCVgNrAHuJqD8/5oM2AEsBh4F7aXFkAN4HfgNVANOAycCxiVvbHAB2Av8C0PAGRzOPAjsCNsMw0ARXYNcA04YsYuAVMCPG/inJ9h/73Ig/PeRHVglQOxDLgetJsGQFfgP6AXUBnYCkwH/rSoyNZkt18BO/PovDc1xgWwqgWxKLNpAMxy6IcCgywLYR9/AtYDC8JRyhOYFsBcE4en3ma2ACoC61xkGxgfn0U41QEYB/zmKPQmT04HzVQBNpqynU4LQLK4D7htNFGRhtcvQD3LQD6KN0pw5gEP3Xe2pQXQFPgL2A8siXD+B2ChUWtXhuiXAXoAreydcsBqp1iNgW4mk/Wdwq2N0f1RgHyZ4/YX2UiiUBegHdDStFgpvG8fEhhPJUmcFErqdCgGgL41xJ4dMCFQg5Ijd4AVVmMrgfEmDmFTfYCeQRYkAfAGpC7TgN5un49wsKbpvrJwKgaAJLa/c1wOajzQmLHI0XIk0M/ti07NRJHOwGgXsFsxdSYx0ZlCmc4GgOYRaXBzK+AHJQQgGbziInjWzksS1ZhEPz3Lpm9IKEQfNbbC7GcDQE1ktxXPRKf970sIIHxMGVEPEe2KOJ2gXiUC4Av43wwK46Op4oujUBSfDwJ9M9RN+IwATLJxRQ0zqwx0Ak5YASpiUcsX8fGY4guf8aqlghycovGJOh3TFrH0XcUVV8DeOdHgcVCjM9BBXVu01Iissds3vp+B1hlGEflS2yS70HxSDZQHlpqUDgPuZXBKkZTkznTj9KfQe+K75iNlUqOGnPwf2B6gpVRpqs1bxQY2s+V9ORPMchIAX8DPQ5GKwhE5q9iLArfZbMhxyXIjJ6NqZMrAW9N3Tbx/x4zhypouSJLqy96BJAD6iJrOPzEdOAjEj9uSRi+V/rlGERWfMiinT1pD1H9SNQG46zJ41A1sX2Oy3NaKV+CLLjZJAHwBdweOJUicHg8weogmha0+T0tFrzpUs5MaFq0kAEI7EEjivzcoyi23bhvF45LiUQ2pPnT/KNbwwgB0id5gNyy9PN+UJU1ENQpo6w6rkSHXpeLWHVsCoF1shQG0B9RcNK/oV9HUDHQzhRfhoS2X0TrRVhiACvEPV3Av3ZWxrkmaeJd2KWqi3g3gQtrDgffbAA3Nj8ji/g6dBdYaz0uo0wAAAABJRU5ErkJggg==" style="vertical-align: middle;">在<img data-latex="E" data-qs-formula="true" src="data:image/png;base64,iVBORw0KGgoAAAANSUhEUgAAABgAAAAZCAYAAAArK+5dAAAAAXNSR0IArs4c6QAAAc5JREFUSEvt1T3ITnEYBvDfS/mKATEoxKAsBoSSjxJlYSGEDJRFiQllIgxiUgbyrZRFBmGySb3voAwGWWSQSEKU8r91vzo9nuec89KTxamzPM9939f/uu7rf50BfX4G+jzfPweYi01YjM14h8t408F8PlZjdv6/D5+ipi2DlXiEC9iPz12knYQz+I4D+DISgGiI5oM4W7O3LZiHY8M1bRiMz6F7sQ4PawCWY0n1EG0AZuAGJiNO+LwGYC2mZ/3PsjYAy/AA97Gn6PuhArAbj4sBnuVvG0vNKwyORKKQ5jxOlgUezSVGfyz1UMrxtherJgZjcCpdsRW3clD0bcNCHCnvtz8FmFZccRNLy3uvWPR9DpqTC9+Fq3Vp0MRgEe5iCDsrABNwGherencDagLYjutd9A/rHs7dvM7Bo4qc4zovYR3A6LwwMWhH1Xrl9BOxKu/EsP5rMKvExaUqkzqA8P21vJmRR09rtB6bjK7gZVuABbhdtH+R+ve0Yobhepyo2Ljxom3AnfR5+L2XFcNpsfBzeNLJspdEVf17WTF6w67Hizxf8Sui6ySambkfiRj5PyWX1pk/U7ECESMfU8Jg+9vTZNO//qL+B2iUsO8S/QAHAVEaFYddbQAAAABJRU5ErkJggg==" style="vertical-align: middle;">上可积，则<img data-latex="\left | {f(x)} \right |" data-qs-formula="true" src="data:image/png;base64,iVBORw0KGgoAAAANSUhEUgAAADcAAAAbCAYAAADYtRcLAAAAAXNSR0IArs4c6QAAA/tJREFUWEfNmFfoT2EYxz9/e1wImSXukEhWyopw4QLZe69CZgpZycgeF0ooMwpZmSHkQraUkXJjJkRmWedbz1unt/M75/yck7z1u/mddzzfZ3yf7/uW8G9GKaAC8CXDcUXvUZLhsLRLKwOTgePAg7SLIubJ1n7AD+AI8DtpLx9cW2AuMAp4n7Q4xfcywFTgFnApxfykKXH7DQQ6ArOAb9rIB9cOWAAMDYx6m3CSDpInmwLvgui8AfaZZ93S7kArYJX3fxKIuO+1g4+LgaXA89BE2dwBmAF8zQJOTtFmfYIITzNvtQcGAU/swJpBna00I55mQROxVuc2NKf9tO+5gasD7AKuAjvsdx+YD3y2w2RA8yA7lgTZ4AzIC6POX2vnOcflBk61eRaYYiB9oysC64A95oC8QLl9SgeEsgh4BOzNO3IjgJ2AUlHR84dSZrmRyYu8kdl+3YDeIQLJJXKqN3lNG4uh5D1/6OABVo9ZelucXxoBK6zNyIG5gKsEbASU98MLtIyJ9l31FtePxHzjARmnVN8O3DVDta4xcBE4GbFPDWCrOfpeVnD1gP5ALQN1G7hsrj1tRjlPq518AtbHuF77zAbWAK+D9Fa0Re93gG323yagbAEnVrF5G6w0colcS1MbqwsYLzIRqCuhYvcxihDU3C8E7URe1xCzHgr64olAps2xqImQxMbKFJ9x3TmK7IGskXMGqs72A2rQ5yIikwZcXWAMIAd9tz16AkeBvsDhFCTkn5NL5CTPBhthPPxLcP4ykZR6pFhYqsdFMw5j7uAcmTQAhpjk8g0oZ8rkZkxa+mtc/ej/cYGE+lBE5EQ2x/JISzGU9OPjsECNMESEIvUuqk4zmgEHTRAsS6P4germPJGQem3mtHRGbElgQh3UxER4Guml+SKPcB0rA2Ya4CghoLrdDMyzXpsZnCv6XpYKhaKiniXD1MP8FNNtQsp9ZCCyh9kdT7eGzl4dy5FdDECUg8TaqtOx1mszgxOZjE5R9Grw6j8LIxRMVWC33crVDtQ/BbS1RVoMXM2Uh5q0emDU8LMjEzg9E0iJ149RJs4IJ2zVkH1aFzP2sEjdCK4tIim1FkVbLKz6cfX0qgCw8kZa6onnbU4mcI5MrqespTbGfEpBdw1KQy5p5qie1einh+RfJnBOmUxKqDdnnLyrG/OpkExLY3jSHGWFZJt6rJq+G0WBExGEC1/e0tuKGu3LJAvsu4TvBBO3H1OuSZomohERSZSHM6IocL9ChS9PCeg1q48kA8LfOwWRbmGsp96XZfhiO7xXUeD06CPK1wOQ7mTPTNgWa6AIpCugd8czGZApzZU5IpHww1DqtMz7aS8DlqKXJj7tFb3j/7zgD7wjMisNlgjkAAAAAElFTkSuQmCC" style="vertical-align: middle;">在<img data-latex="E" data-qs-formula="true" src="data:image/png;base64,iVBORw0KGgoAAAANSUhEUgAAABgAAAAZCAYAAAArK+5dAAAAAXNSR0IArs4c6QAAAc5JREFUSEvt1T3ITnEYBvDfS/mKATEoxKAsBoSSjxJlYSGEDJRFiQllIgxiUgbyrZRFBmGySb3voAwGWWSQSEKU8r91vzo9nuec89KTxamzPM9939f/uu7rf50BfX4G+jzfPweYi01YjM14h8t408F8PlZjdv6/D5+ipi2DlXiEC9iPz12knYQz+I4D+DISgGiI5oM4W7O3LZiHY8M1bRiMz6F7sQ4PawCWY0n1EG0AZuAGJiNO+LwGYC2mZ/3PsjYAy/AA97Gn6PuhArAbj4sBnuVvG0vNKwyORKKQ5jxOlgUezSVGfyz1UMrxtherJgZjcCpdsRW3clD0bcNCHCnvtz8FmFZccRNLy3uvWPR9DpqTC9+Fq3Vp0MRgEe5iCDsrABNwGherencDagLYjutd9A/rHs7dvM7Bo4qc4zovYR3A6LwwMWhH1Xrl9BOxKu/EsP5rMKvExaUqkzqA8P21vJmRR09rtB6bjK7gZVuABbhdtH+R+ve0Yobhepyo2Ljxom3AnfR5+L2XFcNpsfBzeNLJspdEVf17WTF6w67Hizxf8Sui6ySambkfiRj5PyWX1pk/U7ECESMfU8Jg+9vTZNO//qL+B2iUsO8S/QAHAVEaFYddbQAAAABJRU5ErkJggg==" style="vertical-align: middle;">的任何可测子集上也可积。
·正确
·错误
设<img data-latex="f(x)" data-qs-formula="true" src="data:image/png;base64,iVBORw0KGgoAAAANSUhEUgAAADAAAAAZCAYAAAB3oa15AAAAAXNSR0IArs4c6QAAA+dJREFUWEe1l1eIFVkQhr9xVVwDpjWBPgiKGcQFFcQAiqCYEbMiKC6ru6tiFkyIOeeAvph3lw2K6IMPIiIYUAwPZkUQxZwDYjr/UGfoabpv355758Dhwu0+1fVX/fVXnQJKb5UFtD/m8IkKwGfbkWYKcjCe6WgtYAKwBXiUwzfquPO/ApucvSdRdkoDQCVgNrAHuJqD8/5oM2AEsBh4F7aXFkAN4HfgNVANOAycCxiVvbHAB2Av8C0PAGRzOPAjsCNsMw0ARXYNcA04YsYuAVMCPG/inJ9h/73Ig/PeRHVglQOxDLgetJsGQFfgP6AXUBnYCkwH/rSoyNZkt18BO/PovDc1xgWwqgWxKLNpAMxy6IcCgywLYR9/AtYDC8JRyhOYFsBcE4en3ma2ACoC61xkGxgfn0U41QEYB/zmKPQmT04HzVQBNpqynU4LQLK4D7htNFGRhtcvQD3LQD6KN0pw5gEP3Xe2pQXQFPgL2A8siXD+B2ChUWtXhuiXAXoAreydcsBqp1iNgW4mk/Wdwq2N0f1RgHyZ4/YX2UiiUBegHdDStFgpvG8fEhhPJUmcFErqdCgGgL41xJ4dMCFQg5Ijd4AVVmMrgfEmDmFTfYCeQRYkAfAGpC7TgN5un49wsKbpvrJwKgaAJLa/c1wOajzQmLHI0XIk0M/ti07NRJHOwGgXsFsxdSYx0ZlCmc4GgOYRaXBzK+AHJQQgGbziInjWzksS1ZhEPz3Lpm9IKEQfNbbC7GcDQE1ktxXPRKf970sIIHxMGVEPEe2KOJ2gXiUC4Av43wwK46Op4oujUBSfDwJ9M9RN+IwATLJxRQ0zqwx0Ak5YASpiUcsX8fGY4guf8aqlghycovGJOh3TFrH0XcUVV8DeOdHgcVCjM9BBXVu01Iissds3vp+B1hlGEflS2yS70HxSDZQHlpqUDgPuZXBKkZTkznTj9KfQe+K75iNlUqOGnPwf2B6gpVRpqs1bxQY2s+V9ORPMchIAX8DPQ5GKwhE5q9iLArfZbMhxyXIjJ6NqZMrAW9N3Tbx/x4zhypouSJLqy96BJAD6iJrOPzEdOAjEj9uSRi+V/rlGERWfMiinT1pD1H9SNQG46zJ41A1sX2Oy3NaKV+CLLjZJAHwBdweOJUicHg8weogmha0+T0tFrzpUs5MaFq0kAEI7EEjivzcoyi23bhvF45LiUQ2pPnT/KNbwwgB0id5gNyy9PN+UJU1ENQpo6w6rkSHXpeLWHVsCoF1shQG0B9RcNK/oV9HUDHQzhRfhoS2X0TrRVhiACvEPV3Av3ZWxrkmaeJd2KWqi3g3gQtrDgffbAA3Nj8ji/g6dBdYaz0uo0wAAAABJRU5ErkJggg==" style="vertical-align: middle;">在<img data-latex="E" data-qs-formula="true" src="data:image/png;base64,iVBORw0KGgoAAAANSUhEUgAAABgAAAAZCAYAAAArK+5dAAAAAXNSR0IArs4c6QAAAc5JREFUSEvt1T3ITnEYBvDfS/mKATEoxKAsBoSSjxJlYSGEDJRFiQllIgxiUgbyrZRFBmGySb3voAwGWWSQSEKU8r91vzo9nuec89KTxamzPM9939f/uu7rf50BfX4G+jzfPweYi01YjM14h8t408F8PlZjdv6/D5+ipi2DlXiEC9iPz12knYQz+I4D+DISgGiI5oM4W7O3LZiHY8M1bRiMz6F7sQ4PawCWY0n1EG0AZuAGJiNO+LwGYC2mZ/3PsjYAy/AA97Gn6PuhArAbj4sBnuVvG0vNKwyORKKQ5jxOlgUezSVGfyz1UMrxtherJgZjcCpdsRW3clD0bcNCHCnvtz8FmFZccRNLy3uvWPR9DpqTC9+Fq3Vp0MRgEe5iCDsrABNwGherencDagLYjutd9A/rHs7dvM7Bo4qc4zovYR3A6LwwMWhH1Xrl9BOxKu/EsP5rMKvExaUqkzqA8P21vJmRR09rtB6bjK7gZVuABbhdtH+R+ve0Yobhepyo2Ljxom3AnfR5+L2XFcNpsfBzeNLJspdEVf17WTF6w67Hizxf8Sui6ySambkfiRj5PyWX1pk/U7ECESMfU8Jg+9vTZNO//qL+B2iUsO8S/QAHAVEaFYddbQAAAABJRU5ErkJggg==" style="vertical-align: middle;">上可积，则<img data-latex="f(x)" data-qs-formula="true" src="data:image/png;base64,iVBORw0KGgoAAAANSUhEUgAAADAAAAAZCAYAAAB3oa15AAAAAXNSR0IArs4c6QAAA+dJREFUWEe1l1eIFVkQhr9xVVwDpjWBPgiKGcQFFcQAiqCYEbMiKC6ru6tiFkyIOeeAvph3lw2K6IMPIiIYUAwPZkUQxZwDYjr/UGfoabpv355758Dhwu0+1fVX/fVXnQJKb5UFtD/m8IkKwGfbkWYKcjCe6WgtYAKwBXiUwzfquPO/ApucvSdRdkoDQCVgNrAHuJqD8/5oM2AEsBh4F7aXFkAN4HfgNVANOAycCxiVvbHAB2Av8C0PAGRzOPAjsCNsMw0ARXYNcA04YsYuAVMCPG/inJ9h/73Ig/PeRHVglQOxDLgetJsGQFfgP6AXUBnYCkwH/rSoyNZkt18BO/PovDc1xgWwqgWxKLNpAMxy6IcCgywLYR9/AtYDC8JRyhOYFsBcE4en3ma2ACoC61xkGxgfn0U41QEYB/zmKPQmT04HzVQBNpqynU4LQLK4D7htNFGRhtcvQD3LQD6KN0pw5gEP3Xe2pQXQFPgL2A8siXD+B2ChUWtXhuiXAXoAreydcsBqp1iNgW4mk/Wdwq2N0f1RgHyZ4/YX2UiiUBegHdDStFgpvG8fEhhPJUmcFErqdCgGgL41xJ4dMCFQg5Ijd4AVVmMrgfEmDmFTfYCeQRYkAfAGpC7TgN5un49wsKbpvrJwKgaAJLa/c1wOajzQmLHI0XIk0M/ti07NRJHOwGgXsFsxdSYx0ZlCmc4GgOYRaXBzK+AHJQQgGbziInjWzksS1ZhEPz3Lpm9IKEQfNbbC7GcDQE1ktxXPRKf970sIIHxMGVEPEe2KOJ2gXiUC4Av43wwK46Op4oujUBSfDwJ9M9RN+IwATLJxRQ0zqwx0Ak5YASpiUcsX8fGY4guf8aqlghycovGJOh3TFrH0XcUVV8DeOdHgcVCjM9BBXVu01Iissds3vp+B1hlGEflS2yS70HxSDZQHlpqUDgPuZXBKkZTkznTj9KfQe+K75iNlUqOGnPwf2B6gpVRpqs1bxQY2s+V9ORPMchIAX8DPQ5GKwhE5q9iLArfZbMhxyXIjJ6NqZMrAW9N3Tbx/x4zhypouSJLqy96BJAD6iJrOPzEdOAjEj9uSRi+V/rlGERWfMiinT1pD1H9SNQG46zJ41A1sX2Oy3NaKV+CLLjZJAHwBdweOJUicHg8weogmha0+T0tFrzpUs5MaFq0kAEI7EEjivzcoyi23bhvF45LiUQ2pPnT/KNbwwgB0id5gNyy9PN+UJU1ENQpo6w6rkSHXpeLWHVsCoF1shQG0B9RcNK/oV9HUDHQzhRfhoS2X0TrRVhiACvEPV3Av3ZWxrkmaeJd2KWqi3g3gQtrDgffbAA3Nj8ji/g6dBdYaz0uo0wAAAABJRU5ErkJggg==" style="vertical-align: middle;">在<img data-latex="E" data-qs-formula="true" src="data:image/png;base64,iVBORw0KGgoAAAANSUhEUgAAABgAAAAZCAYAAAArK+5dAAAAAXNSR0IArs4c6QAAAc5JREFUSEvt1T3ITnEYBvDfS/mKATEoxKAsBoSSjxJlYSGEDJRFiQllIgxiUgbyrZRFBmGySb3voAwGWWSQSEKU8r91vzo9nuec89KTxamzPM9939f/uu7rf50BfX4G+jzfPweYi01YjM14h8t408F8PlZjdv6/D5+ipi2DlXiEC9iPz12knYQz+I4D+DISgGiI5oM4W7O3LZiHY8M1bRiMz6F7sQ4PawCWY0n1EG0AZuAGJiNO+LwGYC2mZ/3PsjYAy/AA97Gn6PuhArAbj4sBnuVvG0vNKwyORKKQ5jxOlgUezSVGfyz1UMrxtherJgZjcCpdsRW3clD0bcNCHCnvtz8FmFZccRNLy3uvWPR9DpqTC9+Fq3Vp0MRgEe5iCDsrABNwGherencDagLYjutd9A/rHs7dvM7Bo4qc4zovYR3A6LwwMWhH1Xrl9BOxKu/EsP5rMKvExaUqkzqA8P21vJmRR09rtB6bjK7gZVuABbhdtH+R+ve0Yobhepyo2Ljxom3AnfR5+L2XFcNpsfBzeNLJspdEVf17WTF6w67Hizxf8Sui6ySambkfiRj5PyWX1pk/U7ECESMfU8Jg+9vTZNO//qL+B2iUsO8S/QAHAVEaFYddbQAAAABJRU5ErkJggg==" style="vertical-align: middle;">的任何可测子集上也可积。
·正确
·错误

·正确
·错误
设<img data-latex="f(x)" data-qs-formula="true" src="data:image/png;base64,iVBORw0KGgoAAAANSUhEUgAAADAAAAAZCAYAAAB3oa15AAAAAXNSR0IArs4c6QAAA+dJREFUWEe1l1eIFVkQhr9xVVwDpjWBPgiKGcQFFcQAiqCYEbMiKC6ru6tiFkyIOeeAvph3lw2K6IMPIiIYUAwPZkUQxZwDYjr/UGfoabpv355758Dhwu0+1fVX/fVXnQJKb5UFtD/m8IkKwGfbkWYKcjCe6WgtYAKwBXiUwzfquPO/ApucvSdRdkoDQCVgNrAHuJqD8/5oM2AEsBh4F7aXFkAN4HfgNVANOAycCxiVvbHAB2Av8C0PAGRzOPAjsCNsMw0ARXYNcA04YsYuAVMCPG/inJ9h/73Ig/PeRHVglQOxDLgetJsGQFfgP6AXUBnYCkwH/rSoyNZkt18BO/PovDc1xgWwqgWxKLNpAMxy6IcCgywLYR9/AtYDC8JRyhOYFsBcE4en3ma2ACoC61xkGxgfn0U41QEYB/zmKPQmT04HzVQBNpqynU4LQLK4D7htNFGRhtcvQD3LQD6KN0pw5gEP3Xe2pQXQFPgL2A8siXD+B2ChUWtXhuiXAXoAreydcsBqp1iNgW4mk/Wdwq2N0f1RgHyZ4/YX2UiiUBegHdDStFgpvG8fEhhPJUmcFErqdCgGgL41xJ4dMCFQg5Ijd4AVVmMrgfEmDmFTfYCeQRYkAfAGpC7TgN5un49wsKbpvrJwKgaAJLa/c1wOajzQmLHI0XIk0M/ti07NRJHOwGgXsFsxdSYx0ZlCmc4GgOYRaXBzK+AHJQQgGbziInjWzksS1ZhEPz3Lpm9IKEQfNbbC7GcDQE1ktxXPRKf970sIIHxMGVEPEe2KOJ2gXiUC4Av43wwK46Op4oujUBSfDwJ9M9RN+IwATLJxRQ0zqwx0Ak5YASpiUcsX8fGY4guf8aqlghycovGJOh3TFrH0XcUVV8DeOdHgcVCjM9BBXVu01Iissds3vp+B1hlGEflS2yS70HxSDZQHlpqUDgPuZXBKkZTkznTj9KfQe+K75iNlUqOGnPwf2B6gpVRpqs1bxQY2s+V9ORPMchIAX8DPQ5GKwhE5q9iLArfZbMhxyXIjJ6NqZMrAW9N3Tbx/x4zhypouSJLqy96BJAD6iJrOPzEdOAjEj9uSRi+V/rlGERWfMiinT1pD1H9SNQG46zJ41A1sX2Oy3NaKV+CLLjZJAHwBdweOJUicHg8weogmha0+T0tFrzpUs5MaFq0kAEI7EEjivzcoyi23bhvF45LiUQ2pPnT/KNbwwgB0id5gNyy9PN+UJU1ENQpo6w6rkSHXpeLWHVsCoF1shQG0B9RcNK/oV9HUDHQzhRfhoS2X0TrRVhiACvEPV3Av3ZWxrkmaeJd2KWqi3g3gQtrDgffbAA3Nj8ji/g6dBdYaz0uo0wAAAABJRU5ErkJggg==" style="vertical-align: middle;">是可测集<img data-latex="E" data-qs-formula="true" src="data:image/png;base64,iVBORw0KGgoAAAANSUhEUgAAABgAAAAZCAYAAAArK+5dAAAAAXNSR0IArs4c6QAAAc5JREFUSEvt1T3ITnEYBvDfS/mKATEoxKAsBoSSjxJlYSGEDJRFiQllIgxiUgbyrZRFBmGySb3voAwGWWSQSEKU8r91vzo9nuec89KTxamzPM9939f/uu7rf50BfX4G+jzfPweYi01YjM14h8t408F8PlZjdv6/D5+ipi2DlXiEC9iPz12knYQz+I4D+DISgGiI5oM4W7O3LZiHY8M1bRiMz6F7sQ4PawCWY0n1EG0AZuAGJiNO+LwGYC2mZ/3PsjYAy/AA97Gn6PuhArAbj4sBnuVvG0vNKwyORKKQ5jxOlgUezSVGfyz1UMrxtherJgZjcCpdsRW3clD0bcNCHCnvtz8FmFZccRNLy3uvWPR9DpqTC9+Fq3Vp0MRgEe5iCDsrABNwGherencDagLYjutd9A/rHs7dvM7Bo4qc4zovYR3A6LwwMWhH1Xrl9BOxKu/EsP5rMKvExaUqkzqA8P21vJmRR09rtB6bjK7gZVuABbhdtH+R+ve0Yobhepyo2Ljxom3AnfR5+L2XFcNpsfBzeNLJspdEVf17WTF6w67Hizxf8Sui6ySambkfiRj5PyWX1pk/U7ECESMfU8Jg+9vTZNO//qL+B2iUsO8S/QAHAVEaFYddbQAAAABJRU5ErkJggg==" style="vertical-align: middle;">上的非负可测函数，则<img data-latex="f(x)" data-qs-formula="true" src="data:image/png;base64,iVBORw0KGgoAAAANSUhEUgAAADAAAAAZCAYAAAB3oa15AAAAAXNSR0IArs4c6QAAA+dJREFUWEe1l1eIFVkQhr9xVVwDpjWBPgiKGcQFFcQAiqCYEbMiKC6ru6tiFkyIOeeAvph3lw2K6IMPIiIYUAwPZkUQxZwDYjr/UGfoabpv355758Dhwu0+1fVX/fVXnQJKb5UFtD/m8IkKwGfbkWYKcjCe6WgtYAKwBXiUwzfquPO/ApucvSdRdkoDQCVgNrAHuJqD8/5oM2AEsBh4F7aXFkAN4HfgNVANOAycCxiVvbHAB2Av8C0PAGRzOPAjsCNsMw0ARXYNcA04YsYuAVMCPG/inJ9h/73Ig/PeRHVglQOxDLgetJsGQFfgP6AXUBnYCkwH/rSoyNZkt18BO/PovDc1xgWwqgWxKLNpAMxy6IcCgywLYR9/AtYDC8JRyhOYFsBcE4en3ma2ACoC61xkGxgfn0U41QEYB/zmKPQmT04HzVQBNpqynU4LQLK4D7htNFGRhtcvQD3LQD6KN0pw5gEP3Xe2pQXQFPgL2A8siXD+B2ChUWtXhuiXAXoAreydcsBqp1iNgW4mk/Wdwq2N0f1RgHyZ4/YX2UiiUBegHdDStFgpvG8fEhhPJUmcFErqdCgGgL41xJ4dMCFQg5Ijd4AVVmMrgfEmDmFTfYCeQRYkAfAGpC7TgN5un49wsKbpvrJwKgaAJLa/c1wOajzQmLHI0XIk0M/ti07NRJHOwGgXsFsxdSYx0ZlCmc4GgOYRaXBzK+AHJQQgGbziInjWzksS1ZhEPz3Lpm9IKEQfNbbC7GcDQE1ktxXPRKf970sIIHxMGVEPEe2KOJ2gXiUC4Av43wwK46Op4oujUBSfDwJ9M9RN+IwATLJxRQ0zqwx0Ak5YASpiUcsX8fGY4guf8aqlghycovGJOh3TFrH0XcUVV8DeOdHgcVCjM9BBXVu01Iissds3vp+B1hlGEflS2yS70HxSDZQHlpqUDgPuZXBKkZTkznTj9KfQe+K75iNlUqOGnPwf2B6gpVRpqs1bxQY2s+V9ORPMchIAX8DPQ5GKwhE5q9iLArfZbMhxyXIjJ6NqZMrAW9N3Tbx/x4zhypouSJLqy96BJAD6iJrOPzEdOAjEj9uSRi+V/rlGERWfMiinT1pD1H9SNQG46zJ41A1sX2Oy3NaKV+CLLjZJAHwBdweOJUicHg8weogmha0+T0tFrzpUs5MaFq0kAEI7EEjivzcoyi23bhvF45LiUQ2pPnT/KNbwwgB0id5gNyy9PN+UJU1ENQpo6w6rkSHXpeLWHVsCoF1shQG0B9RcNK/oV9HUDHQzhRfhoS2X0TrRVhiACvEPV3Av3ZWxrkmaeJd2KWqi3g3gQtrDgffbAA3Nj8ji/g6dBdYaz0uo0wAAAABJRU5ErkJggg==" style="vertical-align: middle;">必在<img data-latex="E" data-qs-formula="true" src="data:image/png;base64,iVBORw0KGgoAAAANSUhEUgAAABgAAAAZCAYAAAArK+5dAAAAAXNSR0IArs4c6QAAAc5JREFUSEvt1T3ITnEYBvDfS/mKATEoxKAsBoSSjxJlYSGEDJRFiQllIgxiUgbyrZRFBmGySb3voAwGWWSQSEKU8r91vzo9nuec89KTxamzPM9939f/uu7rf50BfX4G+jzfPweYi01YjM14h8t408F8PlZjdv6/D5+ipi2DlXiEC9iPz12knYQz+I4D+DISgGiI5oM4W7O3LZiHY8M1bRiMz6F7sQ4PawCWY0n1EG0AZuAGJiNO+LwGYC2mZ/3PsjYAy/AA97Gn6PuhArAbj4sBnuVvG0vNKwyORKKQ5jxOlgUezSVGfyz1UMrxtherJgZjcCpdsRW3clD0bcNCHCnvtz8FmFZccRNLy3uvWPR9DpqTC9+Fq3Vp0MRgEe5iCDsrABNwGherencDagLYjutd9A/rHs7dvM7Bo4qc4zovYR3A6LwwMWhH1Xrl9BOxKu/EsP5rMKvExaUqkzqA8P21vJmRR09rtB6bjK7gZVuABbhdtH+R+ve0Yobhepyo2Ljxom3AnfR5+L2XFcNpsfBzeNLJspdEVf17WTF6w67Hizxf8Sui6ySambkfiRj5PyWX1pk/U7ECESMfU8Jg+9vTZNO//qL+B2iUsO8S/QAHAVEaFYddbQAAAABJRU5ErkJggg==" style="vertical-align: middle;">上<img data-latex="L" data-qs-formula="true" src="data:image/png;base64,iVBORw0KGgoAAAANSUhEUgAAABUAAAAZCAYAAADe1WXtAAAAAXNSR0IArs4c6QAAAW1JREFUSEvt1MErZlEYx/HPOwsysmDHhiY7Gysmi1mhpjA1KRMadkyKhrIRm2lmMYuZKBOllCKbEZasLGbpD1Bqhpn8A0pIca+O0p3e+77pajZz62zuc873nOf3/J4n5xG+3CMw/RNoA7rQjHJc4Td+4Se+4zKZbbEvjcFbmMMkLtJkKwYa75nCh+h1A1gpVIdioBWYRys6o7WfBbQe6zhFH06ygLZhB98i8ATOs4C+xxcMY7EQMI4X0vQpZtGDl/iRBbQWawHUi6MsoC+whyWMRR49ywJ6p+c4vuYBxhLGGf0JHZeqaVkADaEdu3mg1VHbDoZi3nZaWqFqsIrY/G9wmAf6OvzfuIunQZ8Hf25iJJg/ya3EJ3wOA+Y2ngaN017AND7iOkF8EopXlxwy+aCl4fZRvMJ2AhiPwXeYiWTpT8aT0GfoRiM6gp7LOAjQEjRFsrREY7Aq2O0tju9fWqijirHlX3v+Qx8kW+qhG4ztOhrhShTBAAAAAElFTkSuQmCC" style="vertical-align: middle;">可积.
·正确
·错误
任何无限集均含有一个可数子集
·正确
·错误
设E是[0,1]中的无理点全体，则E中的每一点都是聚点
·正确
·错误
下列结论不正确的是（ ）
····<img src="https://u.qsxt.info/degree/school_4595/39538220_20240113141124466_196.jpg"

····<img src="https://u.qsxt.info/degree/school_4595/39538220_20240113151323103_815.gif"
有理数能表示为纯循环小数的充分必要条件是 ( )
····<img src="https://u.qsxt.info/degree/school_4595/39538220_20240113152222538_906.gif"

····<img src="https://u.qsxt.info/degree/school_4595/39538220_20240113151445916_701.gif"
首页 <上一页 108 109 110 111 112 下一页> 尾页